Answer:
As per the given statement:
The length of an Algebra 2 textbook is 2 times the height.
Let height be x then;
⇒
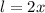 ......[1]; where l is the length.
......[1]; where l is the length.
Also, the sum of the length, width and height of the box is 10 cm.
⇒
 where w is the width. .,.....[2]
where w is the width. .,.....[2]
Substitute equation [1] in [2] we get;
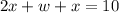 oe
oe
 or
or
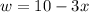 ......[3]
......[3]
(a)
The dimensions of the box is :-
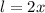
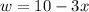
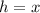
(b)
Volume of the book is given by:
 where V is the volume.
where V is the volume.
Substitute equation [1] and [3] in above formula;
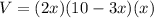
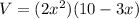
The polynomial function for the volume of the book in the factored form:
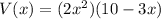
(c)
To find the maximum volume of the book;
we would find the derivative of volume with respect to x i.e,

V(x) =
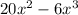 ......[4]
......[4]
Now;
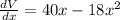
Set this derivative equal to 0.
 or
or

By Zero Product Property states that if ab = 0, then
either a = 0 or b = 0, or we have both a and b are 0.
then we have;
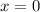 and
and
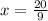
Then substitute these values in equation [4] to get the values of V(x);
 and
and
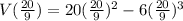 = 32.92(apporx)
= 32.92(apporx)
So, V(x) = 32.92 which is maximum for
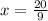
Therefore, the graph of function V(x) is shown below and we can clearly see that there is a maximum very close to 2.22..