Question

Help me I don’t understand it?

Answer 1

let's do 1, 5, 6, 10 and 13.

1)

well, the denominator is the same on each, so we simply have to look at the numerator, who is larger 3 or 5? 3 < 5, 3 is less than 5, so then........
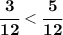
`\bf \cfrac{3}{12}<\cfrac{5}{12}`

5)

`\bf \begin{cases} \cfrac{2}{4}\implies \cfrac{1}{2} \\\\\\ \cfrac{10}{20}\implies \cfrac{1}{2} \end{cases}\qquad \implies \cfrac{2}{4}=\cfrac{10}{20}\implies \cfrac{1}{2}=\cfrac{1}{2}`

6)

we can make both denominators the same if we simply multiply each fraction by the other's denominator.

`\bf \begin{cases} \cfrac{1}{4}\cdot \cfrac{13}{13}\implies \cfrac{13}{52} \\\\\\ \cfrac{4}{13}\cdot \cfrac{4}{4}\implies \cfrac{16}{52} \end{cases}\qquad \implies \cfrac{13}{52}<\cfrac{16}{52}\qquad therefore\qquad \cfrac{1}{4}<\cfrac{4}{13}`

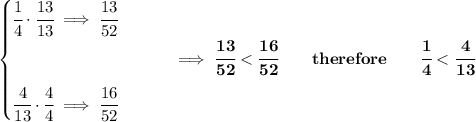
10)

we'll convert the mixed fractions to improper fractions first, then make their denominator the same just like we did in 6).

`\bf \stackrel{mixed}{4(1)/(7)}\implies \cfrac{4\cdot 7+1}{7}\implies \stackrel{improper}{\cfrac{29}{7}}~\hfill \stackrel{mixed}{3(3)/(18)}\implies \cfrac{3\cdot 18+3}{18}\implies \stackrel{improper}{\cfrac{57}{18}} \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \begin{cases} \cfrac{29}{7}\cdot \cfrac{18}{18}\implies \cfrac{522}{126} \\\\\\ \cfrac{57}{18}\cdot \cfrac{7}{7}\implies \cfrac{399}{126} \end{cases}\qquad \implies \cfrac{522}{126}>\cfrac{399}{126}\qquad therefore\qquad 4(1)/(7)>3(3)/(18)`

13)

so both fractions are at a value from 9, so we can simply say, which is larger 2/6 or 4/12?

`\bf \begin{cases} \cfrac{2}{6}\implies \cfrac{1}{3} \\\\\\ \cfrac{4}{12}\implies \cfrac{1}{3} \end{cases}\qquad \implies \cfrac{1}{3}=\cfrac{1}{3}\qquad therefore\qquad 9(2)/(6)=9(4)/(12)`