Answer:
The explicit formula of the given sequence
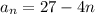
Explanation:
Given A sequence is in an arthmetic progression
The recursive formula
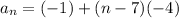
Recursive formula:It is the formula to find the value of
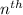 term (
term (
 ) of the sequence when
) of the sequence when
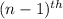 term of the sequence is known .
term of the sequence is known .
Explicit formula:It is the formula to find the value of any term of the sequence when
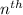 term is known.
term is known.

By simplification
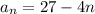
By simplification
Hence, the explicit formula ,
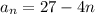 .
.