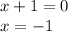Answer:
x = -6 and x= -1
Explanation:
the expression we have is:

Taking tha square of the whole equation:
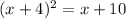
solving the binomial squared on the left side with the rule:
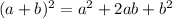
we get:

rearranging all terms to the left:
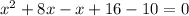
joining like terms:
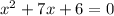
we can sove this quadratic equation with the quadratic formula, or by factoring:
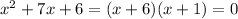
and from this we find our two solutions using the zero product property (if a product of thing is equal to zero, one of them must be zero)
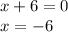
and