Question

In triangle KLM, if K is congruent to L, KL = 9x - 40, LM = 7x - 37, & KM = 3x + 23, find x & the measure of each angle.

Answer 1

x=15, ∠L=∠K=45.7° and ∠M is 77.6°.

Explanation:

Given information: ∠L≅∠K, KL = 9x - 40, LM = 7x - 37, & KM = 3x + 23.

Two angles are congruent, so triangle KLM is an isosceles triangle. Corresponding adjacent sides of congruent angles are equal.

The sides KM and LM are congruent.

`3x+23=7x-37`

Isolate variable terms.

`3x-7x=-23-37`

`-4x=-60`

Divide both sides by -4.

`x=15`

The value of x is 15.

The length of sides of triangle KLM are

`KL=9x-40=9(15)-40=95`

`KM=LM=3(15)+23=45+23=68`

Therefore length of sides are 68, 68 and 95.

Law of cosine

`a^2=b^2+c^2-2bc\cos A`

Using the above formula we get

`K=L=\cos^(-1)((KM^2+KL^2-LM^2)/(2(KM)(KL)))=\cos^(-1)((68^2+95^2-68^2)/(2(68)(95)))=45.69^(\circ)`

`A=\cos^(-1)((LM^2+KM^2-KL^2)/(2(LM)(KM)))=\cos^(-1)((68^2+68^2-95^2)/(2(68)(68)))=77.62^(\circ)`

Therefore, ∠L=∠K=45.7° and ∠M is 77.6°.

Answer 2

The value of x is 15. The measure of angle L and K is 45.7 degree. The measure of angle M is 77.6 degree.

Explanation:

It is given that

`\angle L\cong \angle K`

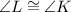
Since two angles are congruent, therefore we can say that the triangle KLM is isosceles triangle.

The sides KM and LM are congruent.

`3x+23=7x-37`

`60=4x`

`15=x`

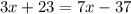
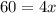
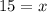
The value of x is 15.

The length of side KL is

`KL=9x-40=9(15)-40=95`

The length of side KM and LM is

`KM=LM=7x-37=7(15)-37=68`

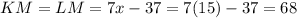
Therefore length of sides are 68, 68 and 95.

Use Law of cosine to find the measure of each angle.

`a^2=b^2+c^2-2bc\cos A`

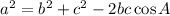
Apply this formula according to the angle.

`L=K=\cos ^(-1)(((KM)^2+(KL)^2-(LM)^2)/(2(KM)(KL))) =\cos ^(-1)((68^2+95^2-68^2)/(2(68)(95)))=45.69^(\circ)`

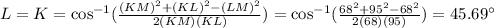
Therefore the measure of angle L and K is 45.7 degree.

The measure of M is calculated as,

`M=\cos ^(-1)(((LM)^2+(KM)^2-(KL)^2)/(2(LM)(KM))) =\cos ^(-1)((68^2+68^2-95^2)/(2(68)(68)))=77.62^(\circ)`

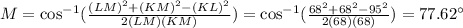
Therefore the measure of angle M is 77.6 degree.