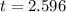Question

A juggler tosses a ball into the air . The balls height, h and time t seconds can be represented by the equation h(t)= -16t^2+40t+4 . Suppose the juggler missed and ball hit the ground . Find the maximum height of the ball and time it took to reach the ground. Round all answers to the nearest hundredth .

Answer 1

The maximum height of the ball is 85.25 feet and it takes 1.25 seconds to reach this height. The ball takes approximately 3.79 seconds to reach the ground.

Step-by-step explanation:

The maximum height of the ball can be found by determining the vertex of the quadratic equation h(t) = -16t² + 40t + 4. The vertex of a quadratic equation in the form h(t) = at² + bt + c is given by the formula t = -b/2a. In this case, a = -16 and b = 40, so the time at which the ball reaches its maximum height is t = -40/(2*(-16)) = 1.25 seconds.

To find the maximum height, substitute this time value back into the equation h(t) = -16t² + 40t + 4: h(1.25) = -16(1.25)² + 40(1.25) + 4 = 31.25 + 50 + 4 = 85.25 feet.

The time it took for the ball to reach the ground can be found by setting h(t) equal to zero and solving for t. The equation -16t² + 40t + 4 = 0 is a quadratic equation that can be solved using the quadratic formula. In this case, the positive root is the appropriate solution, which is t = 3.79 seconds when rounded to the nearest hundredth.

Answer 2

Maximum height is 29 ft

Time to reach the ground is 2.60 seconds

Step-by-step explanation:

We are given equation of height as

`h(t)=-16t^2+40t+4`

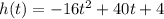
Maximum height:

we know that at maximum height

velocity =0

so, we will find derivative

and then we can set it to 0

and we solve for t

`h'(t)=-32t+40`

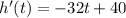
now, we can set it to 0

and then we can solve for t

`h'(t)=-32t+40=0`

`-32t=-40`

`t=(5)/(4)`

`t=1.25`

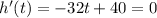
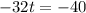
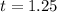
now, we can plug t into height equation

`h((5)/(4))=-16((5)/(4))^2+40((5)/(4))+4`

`h(1.25)=29`

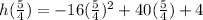
Time to reach the ground:

we know that at ground

height=0

so, we can set h(t)=0

and then we can solve for t

`h(t)=-16t^2+40t+4=0`

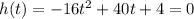
we can use quadratic formula

`t=(-b\pm √(b^2-4ac))/(2a)`

`t=(-40\pm √(40^2-4\left(-16\right)4))/(2\left(-16\right))`

`t=-(√(29)-5)/(4),\:t=(5+√(29))/(4)`

`t=-0.09629,t=2.596`

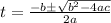
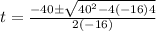
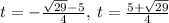
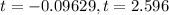
Since, time can never be negative

so, we will only consider positive time

`t=2.596`