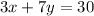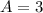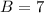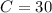Question

Find an equation for the line below. With coordinates (-4,6) and (3,3)

Answer 1

Slope Intercept Form

In decimals:

y=−0.428571x+4.28571

Slope solution

m = -0.428571

Standard Form of a Linear Equation

`A=3`

`B = 7`

`C = 30`

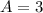
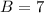
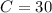
Explanation:

Slope Solution

`m = (rise)/(run) = (\Delta y)/(\Delta x)`

`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (3 - 6)/(3 - -4)`

`m = (-3)/(7)`

`m = -(3)/(7)`

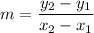
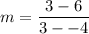
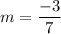
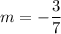
In decimals:

m = -0.428571

Slope intercept form

y=mx+b

by solving for y using the Point Slope Equation.

`y - y_1 = m(x - x_1)`

`y - 6 = -(3)/(7)\left(x + 4\right)`

`y - 6 = -(3)/(7)x + \left(-(3)/(7) * 4\right)`

`y - 6 = -(3)/(7)x +-(12)/(7)`

`y - 6 = -(3)/(7)x -(12)/(7)`

`y = -(3)/(7)x -(12)/(7)+6`

`y = -(3)/(7)x +(30)/(7)`

`m = -(3)/(7)`

`b = (30)/(7)`

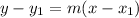
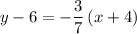
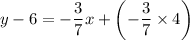
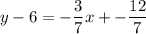
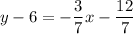
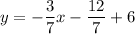
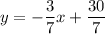
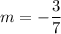
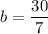
In decimals:

y=−0.428571x+4.28571

Standard Form of a Linear Equation

Ax + By = C

Starting with y = mx + b

`y = -(3)/(7)x +(30)/(7)`

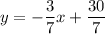
Multiply through by the common denominator, 7, to eliminate the fractions:

`7y = -3x +30`

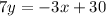
Then rearrange to the Standard Form Equation

`3x+7y=30`

`A=3`

`B = 7`

`C = 30`