Question

`\rm \sum_(k = 0)^n \binom{n}k \frac{ ( - 1 {)}^(k) }{2k + 1} = (2n!!)/((2n + 1)!!) \\`​

Answer 1

Consider the function

`\displaystyle f(x) = \sum_(k=0)^\infty \binom nk ((-1)^k)/(2k+1) x^k`

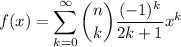
Note that
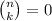`\binom nk=0` when
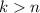`k>n`, so our sum is exactly
`f(1)`.

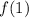Let
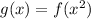`g(x)=f(x^2)`. Then

`\displaystyle x g(x) = \sum_(k=0)^\infty \binom nk ((-1)^k)/(2k+1) x^(2k+1)`

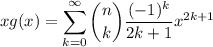
and differentiating both sides reduces the sum to a binomial series,

`\displaystyle x'g(x) + g(x) = \sum_(k=0)^\infty \binom nk (-x^2)^k = \left(1-x^2\right)^n`

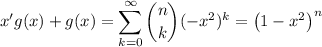
Solve the differential equation for
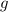`g`. Since
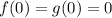`f(0)=g(0)=0`, by the fundamental theorem of calculus we have

`\displaystyle xg(x) = \int_0^x \left(1-t^2\right)^n \, dt \\\\ ~~~~ \implies f(x) = \frac1{\sqrt x} \int_0^(\sqrt x) \left(1-t^2\right)^n \, dt`

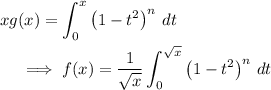
Let
`x\to1` from below.

`\displaystyle f(1) = \int_0^1 \left(1-t^2\right)^n \, dt`

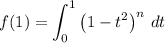
Substitute
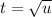`t=\sqrt u` and
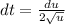`dt=(du)/(2\sqrt u)` to transform this to a beta function integral.

`\displaystyle f(1) = \frac12 \int_0^1 u^(-1/2) (1-u)^n \, du = \frac12\,\mathrm B\left(\frac12, n+1\right)`

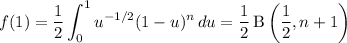
Now we just employ a few beta-gamma and gamma-factorial identities to simplify this result.

`(2n)!! = (2n) (2n-2) (2n-4) \cdots 4\cdot2 = 2^n n!`

`\mathrm B(a,b) = (\Gamma(a) \Gamma(b))/(\Gamma(a+b))`

`\Gamma\left(\frac12\right) = \sqrt\pi`

`\Gamma(n) = (n-1) \Gamma(n-1)`

`\Gamma\left(n+\frac12\right) = ((2n-1)!!)/(2^n) \sqrt\pi`

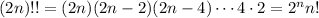
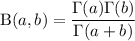
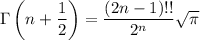
It follows that

`\displaystyle f(1) = \frac12 (\Gamma\left(\frac12\right) \Gamma(n+1))/(\Gamma\left(n+\frac32\right)) \\\\ ~~~~ = \frac12 (\sqrt\pi \, n!)/(\left(n+\frac12\right) \Gamma\left(n+\frac12\right)) \\\\ ~~~~ = (\sqrt\pi \, n!)/((2n+1) ((2n-1)!!)/(2^n) \sqrt \pi) \\\\ ~~~~ = (2^n n!)/((2n+1) (2n-1)!!) \\\\ ~~~~ = \boxed{((2n)!!)/((2n+1)!!)}`