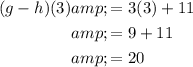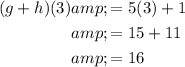Question

G(x) = 4x+6

h(x)=x-5
Write the expressions for (g-h) (x) and (g-h) (x) and evaluate (g- h) (3).
(g-h)(x) =
(g-h)(x) = 0
(g+h)(3) =

Answer 1

`(g-h)(x) = 3x+11`

`(g+h)(x) = 5x+1`

`(g-h)(3) =20`

`(g+h)(3) =16`

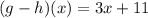
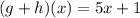
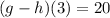
Explanation:

Given functions:

`\begin{cases}g(x)=4x+6\\h(x)=x-5\end{cases}`

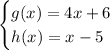
Function composition is an operation that takes two functions and produces a third function.

Therefore, the composite function (g-h)(x) means subtract function h(x) from function g(x). Similarly, (g+h)(x) means to add function h(x) to function g(x).

`\begin{aligned}(g-h)(x) & = g(x)-h(x)\\& = (4x+6)-(x-5)\\& = 4x+6-x+5\\& = 4x-x+6+5\\& = 3x+11\end{aligned}`

`\begin{aligned}(g+h)(x) & = g(x)+h(x)\\& = (4x+6)+(x-5)\\& = 4x+6+x-5\\& = 4x+x+6-5\\& = 5x+1\end{aligned}`

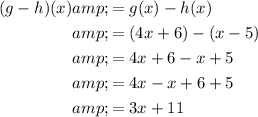
To evaluate both composite functions when x = 3, simply substitute x = 3 into the found composite functions:

`\begin{aligned}(g-h)(3) & = 3(3)+11\\& = 9+11\\&=20\end{aligned}`

`\begin{aligned}(g+h)(3) & = 5(3)+1\\& = 15+11\\&=16\end{aligned}`