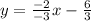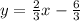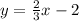Answer:
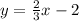
Explanation:
Pre-Solving
We are given the equation 2x - 3y = 6, which we want to get into slope-intercept form.
As the question has told us, slope-intercept form is y=mx+b, where m is the slope and b is the y-intercept.
The equation is currently written in standard form, which is ax+by=c, where a, b, and c are free integer coefficients, but a and b cannot be 0. a is usually non-negative as well.
Solving
We will need to turn standard form into slope-intercept form.
To do this, we need to solve the equation for y, which means that we put the value of y on one side, and everything else on the other.
2x - 3y = 6
Start by subtracting 2x from both sides
2x - 3y = 6
-2x -2x
______________
-3y = -2x + 6
Now, divide by -3.
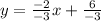
We can simplify this.