Answer:
he solution of the quadratic equation is x=-9 and x =2
So (a) and (f) are correct option
Explanation:
We have given the equation
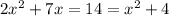
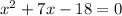
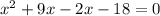

Now taking (x+9) common
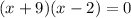
x = -9 and x= 2 are the roots of the equation
So the solution of the quadratic equation is x=-9 and x =2
So (a) and (f) are correct option