Question

Write the standard form of the equation of the circle shown.

Answer 1

`(x+2)^2+(y-2)^2} =13`

Explanation:

We are given a circle with a center at the point (4, -5) and two points on the circle (-5, 0) and (1, 0).

We know that the standard form of equation of a circle is:

`r=√((x_1-x)^2+(y_1-y)^2)`

So putting the given values to get the value of radius (r):

`r=√((-2-1)^2+(2-0)^2)`

`r=√(13)`

Substituting the value of radius to get the equation of the circle:

`√((x+2)^2+(y-2)^2) =√(13)`

Taking square on both the sides:

`(x+2)^2+(y-2)^2} =13`

Therefore, the equation of the given circle is
`(x+2)^2+(y-2)^2} =13`.

Answer 2

The stand form of the circle is

`(x-h)^(2) + (y-k)^(2) = r^(2)`

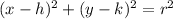
here (h,k) is the center of the cirlce and (x,y) is the point on the circle.

In our case (h,k) is (-2,2)

so our circle equation is

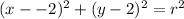`(x--2)^(2) + (y-2)^(2) = r^(2)`. ----------- (i)

and we can find our r by finding the distance between center and the point given on the circle. lets say we take (1,0) point given on the circle according to our diagram

Then

`r = \sqrt{(-2-1)^(2)+(2-0)^(2)}`

`r = √(9+4)`

`r = √(13)`

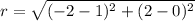
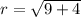
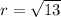
so by putting the values of r in equation (i)

`(x--2)^(2) + (y-2)^(2) = √(13) ^(2)`

`(x+2)^(2) + (y-2)^(2) = 13`

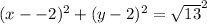
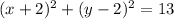
Which is our third option.