Answer:
The correct answer option is A. point B lies inside the circle since CA =
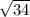 and CB = 4
and CB = 4
Explanation:
We are given a circle with the point C (4,-2) as its center which passes through the point A (1, 3) and we are to figure out if the point B (8, -2) lies inside or outside the circle.
We can find this by using the distance formula:
Distance between C and A =
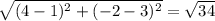
Distance between C and B =
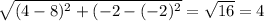
Therefore, the point B lies inside the circle since CA =
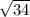 and CB = 4.
and CB = 4.