Question

What % of an object’s mass is below the water line if the object’s density is 0.63g/ml?

Answer 1

According to the Archimedes’ Principle, a body totally or partially immersed in a fluid at rest, experiences a vertical upward thrust equal to the mass weight of the body volume that is displaced.

In this case we have an object partially immersed in water.

If we observe in the image attached, this object does not completely fall to the bottom because the net force acting on it is zero, this means it is in equilibrium.

This is due to Newton’s first law of motion: if a body is in equilibrium the sum of all the forces acting on it is equal to zero

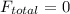`F_(total)=0` (1)

Here, the object experiences two kind of forces:

A force downwards because of its weight:

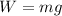`W=mg` (2)

Where
`m` is the mass of the object and
`g` the acceleration of gravity, which in this case (on earth) is
`9.8(m)/(s^(2))`

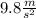
And a force applied upwards because of the buoyancy:

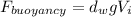`F_(buoyancy)=d_(w)gV_(i)` (3)

Where;

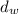`d_(w)` is the density of Water which is
`1(g)/(ml)`

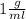
And
`V_(i)` is the volume of the immersed part of the object

Well, if the total net force exerted to the object is zero:

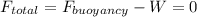`F_(total)= F_(buoyancy)-W=0` Note
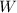`W` has a negative sign because this force is applied downwards

This means the buoyancy is equal to the weight:

`F_(buoyancy)=W` (4)

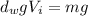`d_(w)gV_(i)=mg` (5)

Dividing by
`g` in both sides:

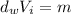`d_(w)V_(i)=m` (6)

Now, the density of an object or fluid is the relation between the mass and the volume, in the case of the object of this problem is:

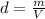`d=(m)/(V)` (7)

Where
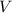`V` is the Volume of the object.

From (7) we can find the mass of the object:

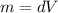`m=dV` (8)

and substitute this value in (6), in order to get a relation between the density of the object and the density of the water, as follows:

`d_(w)V_(i)= dV`

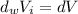
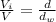`(V_(i))/(V) =(d)/( d_(w))` (9)

`(V_(i))/(V)=(d)/(d_(w))=(0.63g/ml)/(1g/ml)`

Then;

`(0.63g/ml)/(1g/ml)=0.63`

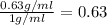
This result is the same as
`(63)/(100)` which represents the
`63\%`

Therefore the answer is:

`63\%` of the mass of the object is below the water line or immersed in water