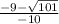Question

Explain why 2x^2+18a=10 has no real number solutions

Answer 1

This equation does have real solutions contrary to your question. They are
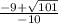`\frac{-9 + √(101)}  {-10}` OR
`\frac{-9 - √(101)}  {-10}`.

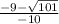Explanation:

In order to prove this has real number solutions, we simply need to use the quadratic formula. To do this, we first need to solve for 0.

2x^2 + 18x = 10

2x^2 + 18x - 10 = 0

Now that we have this and they are all factors of 2, we can divide everything by 2 for ease.

2x^2 + 18x - 10 = 0

x^2 + 9x - 5 = 0

Now we can use the quadratic equation to solve. Remember that A = 1 due to the coefficient of x^2, B = 9 as the coefficient of x and C = -5 as the constant.

`\frac{-b +/- \sqrt{b^(2) - 4ac}}  {2a}`

`\frac{-9 +/- \sqrt{9^(2) - 4(1)(-5)}}  {2(-5)}`

`\frac{-9 +/- √(81 + 20)}  {-10}`

`\frac{-9 +/- √(101)}  {-10}`

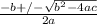
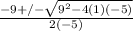
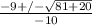
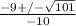
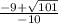`\frac{-9 + √(101)}  {-10}` OR
`\frac{-9 - √(101)}  {-10}`