(4x - 3)(2x - 1) ≥ 0
First, find the zeros:
4x - 3 = 0 2x - 1 = 0
x =
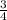 x =
x =

Next, plot these points and choose test points on the outside and between the zeros:
←-------0------
 ------
------
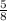 ------
------
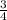 ------1------→
------1------→
Lastly, plug in the test points and look for a positive result (since it is greater than 0).
Test Point 0: [4(0) - 3][2(0) - 1] = ( - )( - ) = + THIS WORKS!
Test Point
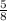 : [4(
: [4(
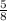 ) - 3][2(
) - 3][2(
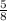 ) - 1] = ( - )( + ) = - This does NOT work
) - 1] = ( - )( + ) = - This does NOT work
Test Point 1: [4(1) - 3][2(1) - 1] = ( + )( + ) = + THIS WORKS!
Answer: x ≤
 or x ≥
or x ≥
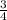
Interval Notation: (-∞,
 ] U [
] U [
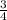 , ∞)
, ∞)
Graph: ←------

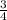 --------→
--------→