Question

What are the restrictions for a? 2a^2+a-15/5a^2+16a+3

Answer 1

a≠ -1/5,a≠ -3

I just did the quick check

Answer 2

The restrictions are

`a\\e -3,a\\e -(1)/(5)`

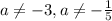
Step-by-step explanation

We were given the rational function,

`(2a^2+a-15)/(5a^2+16a+3)`

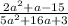
The function is defined for all values of a, except

`5a^2+16a+3=0`

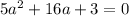
This has become a quadratic trinomial, so we need to split the middle term.

We do that by multiplying the coefficient of
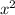`x^2` which is 5 by the constant term which is 3. This gives us 15.

The factors of 15 that adds up to 16 are 1 and 15.

We use these factors to split the middle term.

`5a^2+15a+a+3=0`

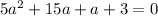
We now factor to get,

`5a(a+3)+1(a+3)=0`

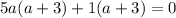
We factor further to get,

`(a+3)(5a+1)=0`

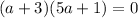
This implies that,

`(a+3)=0,(5a+1)=0`

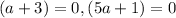
This gives

`a=-3,a=-(1)/(5)`

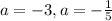
These are the restrictions.