Question

Solve the following system using the Elimination Method; 6x+y=10 and 2x+y=12.

Answer 1

(-1/2, 13)

Explanation:

Multiply the 2nd equation by -1, obtaining the following system:

6x + y = 10

-2x - y = -12

------------------

Combine like terms, obtaining:

6x + y = 10

-2x - y = -12

------------------

4x = -2

Dividing both sides by 4 yields x = -2/4, or x = -1/2

Substituting -1/2 for x in the second equation yields:

2(-1/2) + y = 12, or

-1 + y = 12. Then y = 13, and the solution is

(-1/2, 13)

Answer 2

Hey there!

The solution to the system is
`((1)/(2), 13)`

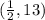
To solve the system, we can multiply the second equation by -1:

`-2x - y = -12`

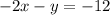
Then, we add the two equations together, and solve for x:

`4x = -2`

`x = (-1)/(2)`

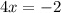
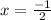
Now, we plug the x value into one of the equations, and solve for y:

`2((1)/(2) ) + y = 12`

`-2 + y = 12`

`y = 13`

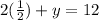
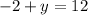
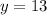
Now we know that the solution to the system is
`((1)/(2), 13)`

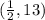
Hope it helps and have an amazing day!