Question

Write an equation in slope-intercept form of the line that passes through the given point and is parallel to the graph of the given equation.


`(2, -1 )(-3)/(2) x + 6`

Write an equation in slope-intercept form of the line that passes through the given point and is parallel to the graph of the given equation.

`(4,2) ; x= -3`

Write an equation in slope-intercept form of the line that passes through the given point and is perpendicular to the graph of the given equation.

`(-2,3) ; y=(1)/(2) x-1`

Answer 1

1) Given equation:
`y=(-3)/(2) x + 6`.

Slope of the given equation =
`-(3)/(2)`.

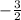Parallel lines have equal slopes.

Therefore, slope of parallel line is also
`-(3)/(2)`.

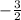Given point (2,-1).

Applying point slope form y-y1 = m(x-x1)

y - (-1) =
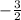`-(3)/(2)`(x-2)

y+1 =
`-(3)/(2)x+3`

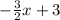
Subtracting 1 from both sides, we get

`y= -(3)/(2)x+2`.

2) Given equation x=-3.

The given line is a vertical line.

Therefore, parallel line would also be a vertical line.

For the given point (4,2) we would have equation for vertical line x = 4.

Therefore, required equation of line is x = 4.

3) Given equation:
`y=(1)/(2) x -1`.

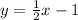Slope of the given line is :
`(1)/(2)`.

Slope of perpendicular line is negative reciprocal.

Therefore, slope of perpendicular line = -2.

Given point (-2,3).

Applying point-slope form, we get

y-3 = -2(x-(-2))

y -3 = -2 (x+2)

y -3 = -2x -4 .

Adding 3 on both sides, we get

y = -2x -1.

Therefore, equation of perpendicular line is y = -2x -1.