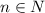Question

An arithmetic sequence is defined by the recursive formula t1 = 11, tn = tn - 1 - 13, where n ∈N and n > 1. Which of these is the general term of the sequence? A) tn = 11 - 13(n - 1), where n ∈N and n > 1 B) tn = 11 - 13(n - 2), where n ∈N and n ≥ 1 C) tn = 11 - 13(n - 1), where n ∈N and n ≥ 1 D) tn = 11 - 13(n + 1), where n ∈N and n ≥ 1

Answer 1

ANSWER

The general term of the sequence is.


`t_n= 11 - 13(n - 1)`

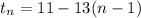
The correct answer is C.

Step-by-step explanation
The recursive definition of the sequence is given by


`t_n=t_(n-1)-13`
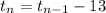
where

`t_1=11`

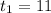
and

`n > 1.`

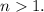
When we plug in

`n = 2`
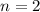
into the recursive definition, we obtain,


`t_2=t_(2-1)-13`



`\Rightarrow t_2=t_(1)-13`


`\Rightarrow \: t_2=11-13`


`t_2= - 2`

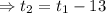
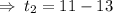
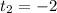
The Commons difference is

`d = - 2 - 11 = - 13`

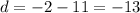
The general term is given by the formula,


`t_n= t_1 + (n - 1)d`

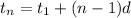
We substitute the above values to obtain,


`t_n= 11 + (n - 1)( - 13)`

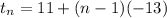
This implies that,


`t_n= 11 - 13(n - 1)`

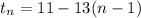
where,

`n\in N`