Answer:
f(x) = |x|
f(x) = |x| + 3
f(x) = |x| - 6
Explanation:
The parent function for all the given functions is the modulus function f(x)=|x|.
A modulus function gives the absolute value of a number or variable.
The absolute value of a number is its positive numerical value.
Therefore, the range of f(x)=|x| is more than or equal to zero.
The graph of f(x)=|x| is:
- Line y = x where x ≥ 0
- Line y = -x where x ≤ 0
- Vertex at (0, 0)
Translations

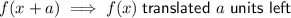

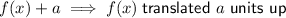

For a modulus function to have a vertex with an x-value of zero after translation, the function can only be translated up or down. If it was translated left or right, the x-value of the vertex would no longer be zero.
Therefore:
f(x) = |x| → No translation. Vertex at (0, 0).
f(x) = |x| + 3 → Translated 3 units up. Vertex at (0, 3).
f(x) = |x + 3| → Translated 3 units left. Vertex at (-3, 0).
f(x) = |x| - 6 → Translated 6 units down. Vertex at (0, -6).
f(x) = |x + 3| - 6 → Translated 3 units left and 6 units down. Vertex at (-3, -6).
So the functions that have a vertex with an x-value of zero are:
- f(x) = |x|
- f(x) = |x| + 3
- f(x) = |x| - 6