Answer:
Option B -
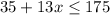 ; 10 people
; 10 people
Explanation:
Given : Morgan is arranging a bowling party for his friends.
To find : What is the maximum number of people that Morgan can invite to stay under his budget of $175 identify the inequality to solve and the maximum number of people ?
Solution :
Let the number of people could be invited to the party be 'x'.
The bowling alley also charges $13 for each person who attends the party.
The cost of x people will be $13x.
The party room at the bowling alley is $35.
The maximum number of people that Morgan can invite to stay under his budget of $175.
The inequality form is
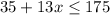
Solving the inequality,
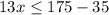
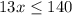
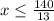
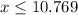
The required number of people will be 10.
Therefore, option B is correct.