Answer:
Since
 , the ball is going to pass through the hoop.
, the ball is going to pass through the hoop.
Explanation:
We have the following function.
 .
.
If the center of the hoop is located at (12, 10), will the ball pass through the hoop?
This is going to happen if
 . We have to apply f(12) in the equation and verify the result. So:
. We have to apply f(12) in the equation and verify the result. So:
 .
.
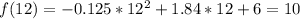 .
.
Since
 , the ball is going to pass through the hoop.
, the ball is going to pass through the hoop.