Question

What is the range of the exponential function shown below

Answer 1

The correct option is C.

Explanation:

Range is the set of output or the values of the function.

The given function is

`f(x)=9\cdot 2^x`

If a exponential function is defined as g(x)=a^x, where a>0, then the value of g(x) is always greater than 0, g(x)>0.

It means,

`2^x>0`

Multiply both sides by 9.

`9\cdot 2^x>9\cdot 0`

`9\cdot 2^x>0`

`f(x)>0`

The value of the function f(x) is always greater than 0, therefore the range of the function is

Range = y>0

Hence the correct option is C.

Answer 2

Answer : y>0

f(x) = 9*2^x

f(x) is an exponential function

`f(x) = 9*2^x`

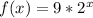
When we plug in positive value for x , the value of y is positive

When we plug in negative value for x , the value y is also positive

So for any value of x, the y value is positive always.

Range is the set of y values for which the function is defined

y values are positive , so range is y >0