Question

Jason inherited a piece of land from his great-uncle. Owners in the area claim that there is a 45% chance that the land has oil. Jason decides to test the land for oil. He buys a kit that claims to have an 80% accuracy rate of indicating oil in the soil. If the test predicts that there is no oil, what is the probability after the test that the land has oil?

Answer 1

The options are

A.

0.1698

B.

0.2217

C.

0.5532

D.

0.7660

Answer 2

Answer: The probability after the test that the land has oil is 0.09.

Step-by-step explanation:

Let A is the event that the land has oil.

It is given that there is a 45% chance that the land has oil. So,

`P(A)=(45)/(100)`

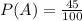
The probability that the land has no oil is,

`P(A)=[tex]P(A')=1-P(A)=1-(45)/(100)=(100-45)/(100)=(55)/(100)`

Let B is the event that the kit gives the accurate rate of indicating oil in the soil. So,

`P(B)=(80)/(100)`

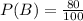
The probability that the kit gives the false result is,

`P(B')=1-P(B)=1-(80)/(100)=(100-80)/(100)=(20)/(100)`

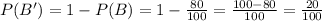
Events A and B are two independent events and we have to find the probability that the last has oil and kit given false result.

`P(A\cap B')=P(A)P(B')`

`P(A\cap B')=((45)/(100))((20)/(100))=(900)/(10000) =(9)/(100)=0.09`

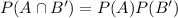
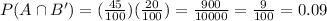
Therefore, the if the test predicts that there is no oil, then the probability after the test that the land has oil is 0.09.