Question

An isosceles triangle has angle measures 50°, 50°, and 80°. The side across from the 80° angle is 10 inches long. How long are the other sides?

Answer 1

7.78 on apex :))))

Step-by-step explanation:

Answer 2

Answer: The value of other side is 7.8 inch.

Step-by-step explanation:

It is given that the isosceles triangle has angle measures 50°, 50°, and 80°. The side across from the 80° angle is 10 inches long.

Let the given length of other equal sides be x.

The side across from the 50° angle is x inches long.

Law of sine,

`(a)/(\sin A)= (b)/(\sin B) =(c)/(\sin C)`

`(x)/(\sin (50))= (10)/(\sin (80))`

`(x)/(0.766) =(10)/(0.9848)`

`x =(10)/(0.9848)* (0.766)`

`x =7.778229 \approx 7.8`

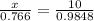
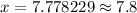
Therefore, the value of other side is 7.8 inch.