frational roots are those numbers that can be written in form
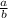 where a and b are integers (integers are like -5,-4,-3,-2,-1,0,1,2,3,4, etc)
where a and b are integers (integers are like -5,-4,-3,-2,-1,0,1,2,3,4, etc)
some examples are 1=1/1, 2=2/2, -4=-4/1, 4/3, 0.111111111111=1/9, etc
irrational numbers are numbers that can't be written that way like pi
numbers that involve √-1 or a square root of any negative number are called complex numbers and are neither rational nor irrational.
roots are the values of x that makes the function equal to 0
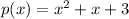
set equal to 0

I can't factor so use quadratic formula
for

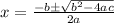
so

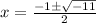
√-11 is a square root of a negative number so it is a complex number. therefore, the function does not have rational or irrational roots
p(x) has no rational or irrational roots