Question

Domain and Range for the function f(x)=5IXI is

Answer 1

The domain of the function f(x) is:

`\mathrm{Domain\:of\:}\:5\left|x\right|\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<x<\infty \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:\infty \:\right)\end{bmatrix}`

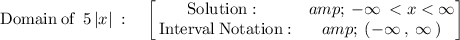
The range of the function f(x) is:

`\mathrm{Range\:of\:}5\left|x\right|:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)\ge \:0\:\\ \:\mathrm{Interval\:Notation:}&\:[0,\:\infty \:)\end{bmatrix}`

Explanation:

Given the function

`f\left(x\right)=5\left|x\right|`

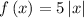
Determining the domain:

We know that the domain of the function is the set of input or arguments for which the function is real and defined.

In other words,

• Domain refers to all the possible sets of input values on the x-axis.

It is clear that the function has undefined points nor domain constraints.

Thus, the domain of the function f(x) is:

`\mathrm{Domain\:of\:}\:5\left|x\right|\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:-\infty \:<x<\infty \\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:\infty \:\right)\end{bmatrix}`

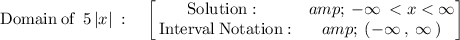
Determining the range:

We also know that range is the set of values of the dependent variable for which a function is defined.

In other words,

• Range refers to all the possible sets of output values on the y-axis.

We know that the range of an Absolute function is of the form

`c|ax+b|+k\:\mathrm{is}\:\:f\left(x\right)\ge \:k`

`k=0`

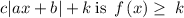
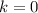
so

Thus, the range of the function f(x) is:

`\mathrm{Range\:of\:}5\left|x\right|:\quad \begin{bmatrix}\mathrm{Solution:}\:&\:f\left(x\right)\ge \:0\:\\ \:\mathrm{Interval\:Notation:}&\:[0,\:\infty \:)\end{bmatrix}`