Question

In this diagram, what is ac?

Answer 1

`\sqrt{17 {}^(2) { - 8}^(2) } = 15 \\ 21 - 15 = 6 \\ \sqrt{8 { }^(2) } + √(6 ) {}^(2) = 10 \\ c.10`

Answer 2

AC = 10 units .

Explanation:

Given : Triangle ABC.

To find : What is AC.

Solution : We have given Triangle ABC.

Triangle BCD is right angle triangle .

By the Pythagorean theorem :

`(BC)^(2) = (BD)^(2) + (CD)^(2)`.

Plug the values .

`(17)^(2) = (BD)^(2) + (8)^(2)`.

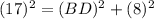289 =
`(BD)^(2) + 64`.

On subtractin g 64 from both sides.

289 - 64 =
`(BD)^(2)`.

225 =
`(BD)^(2)`.

Taking square root .

BD =
`√(225)`.

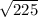BD 15 units .

AB = AD+ BD

21 = AD + 15

AD = 21 -15

AD = 6 units .

Now , Triangle ACD is right angle triangle .

`(AC)^(2) = (6)^(2) + (8)^(2)`.

`(AC)^(2) = 36 +64`.

`(AC)^(2) =  100`.

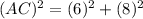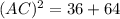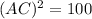Taking square root

AC = 10 units .

Therefore, AC = 10 units .