Question

What’s the answer??(SOMEONE PLEASE HELP ME)

Answer 1

We know that According to Algebra of Real Functions :

If f and g are two real functions which are defined under the same domain then
`((f)/(g))(x) = (f(x))/(g(x))`

`\implies Given\;Function\;is\;(-1)/(x√(3x - 9))`

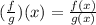
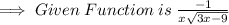
Now we need find the Domain of this Function :

The Condition for Square Root to be defined is any Expression under it should be Greater than or Equal to Zero.

When Function is a Fraction, it Cannot be defined when the denominator becomes zero. Because when the denominator is zero, the fraction tends to ∞ (because anything divided by zero tends to ∞)

According to Above Conditions Described above, The Given Function is Definable only when the Expression which is under the Square Root is Greater than Zero and x ≠ 0

⇒ 3x - 9 > 0

⇒ 3x > 9

⇒ x > 3

⇒ The Domain of the Given Function is (3 , ∞)

1st Option is the Answer