Question

WHERE DOES THE PYTHAGOREAN IDENTITY SIN2 Θ + COS2 Θ = 1 COME FROM? HOW WOULD YOU USE IT TO FIND THE SINE COSINE AND TANGENT VALUES OF THE ANGLE?

Answer 1

Consider right triangle ABC wit hright angle C. Then by the Pythagorean theorem,

`AB^2=AC^2+BC^2.`

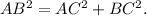
Divide this equality by
`AB^2:`

`(AB^2)/(AB^2)=(AC^2)/(AB^2)+(BC^2)/(AB^2),\\ \\1=\left((AC)/(AB)\right)^2+\left((BC)/(AB)\right)^2.`

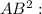
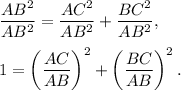
Note that

`(AC)/(AB)=\cos \angle A,\\ \\(BC)/(AB)=\sin \angle A.`

Then

`1=\cos^2 \angle A+\sin^2 \angle A.`

Suppose that you know the sine of the angle, then tha cosine of the angle can be determined as

`\cos \angle A=\pm√(1-\sin^2 \angle A).`

If you divide the equality
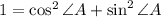`1=\cos^2 \angle A+\sin^2 \angle A` by the
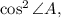`\cos ^2 \angle A,` you get

`(1)/(\cos^2 \angle A)=1+\tan^2 \angle A\Rightarrow \tan^2 \angle A=(1)/(\cos^2 \angle A)-1.`