Question

The perimeter of AABC is 13 cm. It was dilated to

create A'B'C'.
What is the perimeter of A'B'C'?
13 cm
A
C
26 cm
39 cm
A
с
52 cm
0
5
B
15
В"

Answer 1

Given:

Consider the below figure attached with this question.

Perimeter of triangle ABC is 13 cm.

Triangle ABC is dilated to create the triangle A'B'C'.

To find:

The perimeter of triangle A'B'C'.

Solution:

We know that, dilated figures are similar.

`\text{Scale factor}=\frac{\text{Side of image}}{\text{Corresponding side of preimage}}`

`\text{Scale factor}=(OB')/(OB)`

`\text{Scale factor}=(5+15)/(5)`

`\text{Scale factor}=(20)/(5)`

`\text{Scale factor}=4`

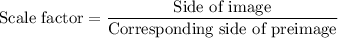
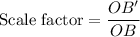
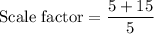
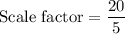
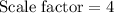
Perimeters of similar figure is proportional to the corresponding sides of that figure or equal to the scale factor.

`\frac{\text{Perimeter of }\Delta A'B'C'}{\text{Perimeter of }\Delta ABC}=\text{Scale factor}`

`\frac{\text{Perimeter of }\Delta A'B'C'}{13}=4`

Multiply both sides by 13.

`\text{Perimeter of }\Delta A'B'C'=13* 4`

`\text{Perimeter of }\Delta A'B'C'=52`

Therefore, the perimeter of triangle A'B'C' is 52 cm.

Note: Options names are not in correct form.