Answer:
D.
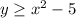
Explanation:
Since, the parabola is shifted 5 units down from the origin.
We get the graph of the function is given by
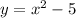 .
.
In order to find the inequality, we will use the 'Zero Test'.
Now, this test states that after substituting the point ( x,y ) = ( 0,0 ) in the given equation, if:
1. This point satisfy the equation, then the solution region is towards the origin.
2. This point does not satisfy the equation, the solution region is away from the origin.
As, from the given graph we see that the solution region is towards the origin.
This means that the this equation satisfies the 'Zero Test' and since
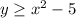 gives 0 ≥ -5, which is true.
gives 0 ≥ -5, which is true.
So, we get the inequality as
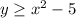 .
.
Hence, option C is correct.