A ball is fired with speed v = 180 m/s at an angle 40 degree
So here we can say the components of velocity is given as
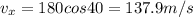
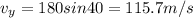
now when ball will reach the maximum height its velocity in vertical direction will become zero
so here we can say
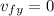
now using kinematics we will have
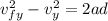
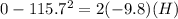
so maximum height is
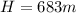
so it will reach at maximum height of 683 m