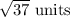Question

Find the length of the diagonal BD in the quadrilateral ABCD shown in the coordinate plane ?

Answer 1

bearing in mind B is at (4,3) and D is at (-2,-4).

`\bf ~~~~~~~~~~~~\textit{distance between 2 points} \\\\ B(\stackrel{x_1}{4}~,~\stackrel{y_1}{3})\qquad D(\stackrel{x_2}{-2}~,~\stackrel{y_2}{-4})\qquad \qquad d = √(( x_2- x_1)^2 + ( y_2- y_1)^2) \\\\\\ BD=√((-2-4)^2+(-4-3)^2)\implies BD=√((-6)^2+(-7)^2) \\\\\\ BD=√(36+49)\implies BD=√(85)`

Answer 2

Answer:
`√(37)\text{ units}`

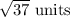
Explanation:

Distance formula : The distance between two points P(a,b) and Q(c,d) is given by :-

`d=√((d-b)^2+(c-a)^2)`

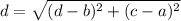
From the graph , the coordinated of point B = (4,3)

and the coordinates of D = (-2,4)

Then ,
`BD=√((4-3)^2+(-2-4)^2)`

`BD=√((1)^2+(-6)^2)=√(1+36)=√(37)\text{ units}`

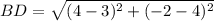
Hence, the length of the diagonal BD in the quadrilateral ABCD =
`√(37)\text{ units}`