Question

A population of insects grows exponentially, as shown in the table. Suppose the increase in population continues at the same rate.

What is the insect population at the end of week 11?

Round to the nearest whole number.

Enter your answer in the box.

Answer 1

Answer: 1730

Explanation:

Answer 2

We are told that a population of insects grows exponentially and we are given a table of data about insect population growth. We are asked to find population of insects at the end of week 11.

The initial insect population is 20 and at the end of 1st week population increases to 30.

Let us find growth percentage of insect population,

`\text{Growth percentage}=\frac{\text{Difference}}{\text{Actual}}\cdot100`

`\text{Insect growth percentage}=(30-20)/(20) \cdot 100`

`\text{Insect growth percentage}=(10)/(20) \cdot 100`

`\text{Insect growth percentage}=50`

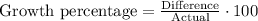
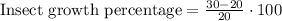
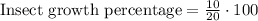
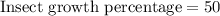
We can see that insect population is growing at rate of 50% per week.

Now let us write an exponential function for our population.

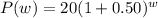`P(w)=20(1+0.50)^(w)`, where P(w) represents population at the end of w weeks.

Let us substitute w=11 in our function to find insect population at the end of 11 weeks.

`P(11)=20(1+0.50)^(11)`

`P(11)=20(1.50)^(11)`

`P(11)=20\cdot 86.49755859375`

`P(11)=1729.951171875\approx 1730`

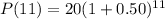
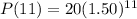
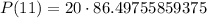
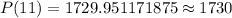
Therefore, population of insects at the end of 11th week will be 1730.