Question

The image of a triangle after it has been dilated with a center at the origin has vertices at A’(-12,6) B’(6,-18) and C’ if the pre-image of A ‘Point Ahas coordinates of (-18,9) and the pre- image of C point C has coordinates of (18,12) which statements are true ? Check All that apply •The coordinates of C are (27,18) •the coordinates for C are (12,8) •the scale factor is 1.5 •the scale factor is 0.75 •the scale factor is 2/3 •the coordinates of B are (9,-27) •the coordinates of B are (4,-12)

Answer 1

• scale factor is 2/3.

• coordinates of B are (9,-27).

• coordinates of C' are : (12,18)

Explanation:

The image of a triangle after it has been dilated with a center at the origin has vertices at A’(-12,6) B’(6,-18) and C’ .

Point A has coordinates of (-18,9) and the pre- image of C' point C has coordinates of (18,12).

Clearly when we compare point A and point A' we see that the transformation is a dilation.

let the scale factor of dilation is 'k'.

i.e. A→ A'

i.e. k(-18,9)=(-12,6)

(-18k,9k)=(-12,6)

i.e. -18k=-12

and 9k=6

Hence, on solving we get:

k=2/3

i.e. the scale factor is 2/3.

Also,

we find the coordinates of B(c,d) by:

2/3(c,d)=(6,-18) since B→ B'

2/3×c=6

Hence c=9

and 2/3 ×d=-18

d=-27.

Hence, the coordinates of B are (9,-27).

Also the coordinates of C are (18,12)

Hence, coordinates of C' are:

`((2)/(3)* 18,(3)/(2)* 12)\\\\=(12,18)`

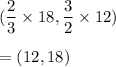
Hence, the coordinates of C' are : (12,18)