Question

Four cups of a salad blend containing 40% spinach is mixed with an unknown amount of a salad blend containg 55% spinach. The resulting salad contains 50% spinach. How many cups of salad are in the resulting mixture?

Answer 1

Option C: 12 cups of salad

Let the unknown cups of salad in the mixture be x( unknown cup in 55% mixture)

Thus, we have the following expression that shows the number of salad in the resulting mixture;

4(40%) + x(55%) = (4+x)(50%)

= 0.4(4) + x(0.55) = 0.5(4 + x)

= 1.6 + 0.55x = 0.2 + 0.5x

0.2 -1.6 = 0.55x-0.5x

0.4 = 0.05x

x = 0.4/0.05

x = 8 cups of salad

So the number of salad cups in the resulting mixture = x + 4 = 8 + 4 = 12 cups of salad

Answer 2

Answer: 12 cups of salad blend are in the resulting mixture

Step-by-step explanation:

Since we have given that

4 cups of a salad blend contains 40% spinach

Using mixture allegation method, we get that

8 cups of a salad blend contains 55% spinach as shown in the figure below.

Now, we need to find the number of cups of salad in the resulting mixture,

`0.4* 4+0.55* 8=0.5* x\\\\1.6+4.4=0.5x\\\\6=0.5x\\\\(6)/(0.5)=x\\\\12=x`

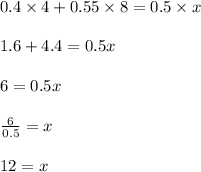
Hence, 12 cups of salad blend are in the resulting mixture .