Question

In △ABC, AB=8, BC=10, and AC=12. Let M, N, and K be the midpoints of the sides of △ABC. Find length of each side of △MNK. No picture.

Answer 1

Answer: The length of MN is 6, length of NK is 4 and Length of MK is 5.

Step-by-step explanation:

It is given that In △ABC, AB=8, BC=10, and AC=12. Let M, N, and K be the midpoints of the sides of △ABC.

The mid point theorem states that if a line segment joining the midpoints of two sides of the triangle, then the length of that line is half of the length of third line.

If M and N are mid points of AB and BC respectively, then the line MN must be parallel to AC and the length of MN is half of the length of AC.

`MN=(12)/(2) =6`

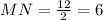
If N and K are mid points of BC and AC respectively, then the NK line must be parallel to AB and the length of NK is half of the length of AB.

`NK=(8)/(2) =4`

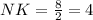
If M and K are mid points of AB and AC respectively, then the line MK must be parallel to BC and the length of MK is half of the length of BC.

`MK=(10)/(2) =5`

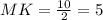
Therefore, the length of MN is 6, length of NK is 4 and Length of MK is 5.