Question

Based on the given angle measures, which triangle has side length measures that could be correct?

Answer 1

The answer is D on edgen.

Explanation:

D. the 4th figure

Answer 2

The triangle in the figure 4 is correct .

Reason

by using the trignometric identity

`tan\theta = (Perpendicular)/(Base)`

Thus

`tan 30^(\circ) = (Perpendicular)/(Base)`

`tan 30 ^(\circ) =(1)/(√(3))`

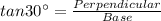
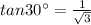
Now in the figure (1)

`tan 30^(\circ) = (13.9)/(8)`

`(1)/(√(3)) = (13.9)/(8)`

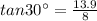
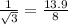
on simplify

`0.5774 \\eq 1.7375`

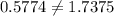
thus side length measures in the figure (1) is not correct .

Now in the figure (2)

`tan30^(\circ) =(16)/(8) \\ (1)/(√(3)) =(16)/(8) \\ 0.577 \\eq 2`

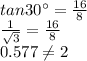
thus side length measures in the figure (2) is not correct .

Now in the figure (3)

`tan 30 ^(\circ) = (8)/(16) \\ (1)/(√(3)) =(8)/(16) \\ 0.577\\eq0.5`

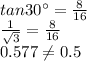
thus side length measures in the figure (3) is not correct .

Now in the figure (4)

`tan30^(\circ) = (8)/(13.9) \\ (1)/(√(3)) =(8)/(13.9)\\ 0.577 = 0.576(approx)`

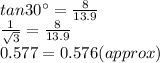
Therefore the figure (4) is correct triangle has side length measures that could be correct

Hence proved