Answer:
0.236J
Step-by-step explanation:
Given: collision between a hammer and a nail, it is approximately elastic.a 550 g hammer moving with an initial speed of 3.5 m/s struck a 10g nail.
To Find: Kinetic Energy acquired by nail.
Solution: Let mass and initial speed of hammer be=
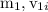
final speed of hammer=
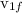
mass and initial speed of nail be=
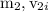
final speed of nail=
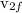
momentum before collision
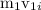 +
+
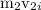
momentum after collision
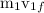 +
+
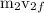
as collision is elastic momentum is conserved
momentum before collision = momentum after collision
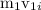 +
+
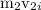 =
=
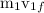 +
+
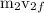
as nail was at rest initially ,
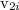 =
=
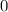
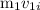 =
=
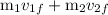
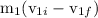 =
=
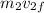
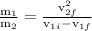
kinetic energy before collision
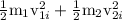
kinetic energy after collision
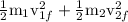
As in elastic collision Kinetic energy remains conserved
kinetic energy before collision= kinetic energy after collision
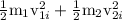 =
=
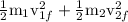
given,
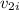 =
=
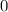
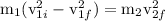
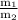 =
=
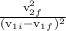
putting value of
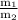 from previous equation
from previous equation
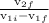 =
=
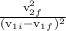
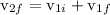
putting it in equation of momentum, we get
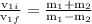
putting values
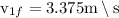
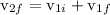
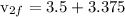
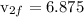
Kinetic energy acquired by nail =
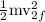
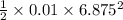
0.236 J
Hence Kinetic Energy acquired by nail is 0.236 J