Answer-
For side length of 3.56 cm and height of 7.10 cm the cost will be minimum.
Solution-
Let us assume that,
x represents the length of the sides of the square base,
y represent the height.
Given the volume of the box is 90 cm³, so
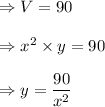
As the top and bottom cost $0.60 per cm² and the sides cost $0.30 per cm². Total cost C will be,

Then,
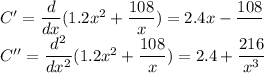
As C'' has all positive terms so, for every positive value of x (as length can't be negative), C'' is positive.
So, for minima C' = 0
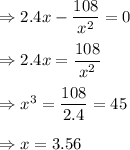
Then,
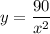
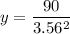
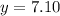
Therefore, for side length of 3.56 cm and height of 7.10 cm the cost will be minimum.