Look at the picture.
We have the equation (1) 12x + 4y = 40.
We know, the sum of the acute angles in a right triangle is 90°.
Therefore we have the equation (2) (12x + 4y) + (17x - y) = 90
Substitute (1) to (2):
40 + 17x - y = 90 subtract 40 from both sides
17x - y = 50 (3)
We have the system of equations:
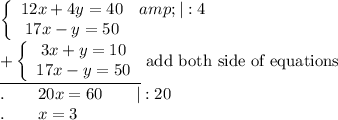
Substitute the value of x to (3)
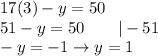
Answer: x = 3 and y = 1.