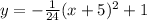Question

Derive the equation of the parabola with a focus of (-5,-5) and a directrix of y=7.

Answer 1

`y=-(1)/(24)(x+5)^2+1`

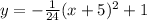
Explanation:

The given parabola has its focus at (-5,-5) and the directrix is at: y=7.

The equation of such parabola is given by the formula:

`(x-h)^2=-4p(y-k)`

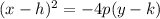
The vertex of the parabola is the midpoint of (-5,-5) and (-5,7).

`((-5+-5)/(2),(-5+7)/(2) )=(-5,1)`

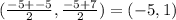
The value of p is the distance from the (-5,-5) to (-5,1).

p=|1--5|=6

We substitute the values of the vertex and p into the equation to get;

`(x--5)^2=-4(6)(y-1)`

`(x+5)^2=-24(y-1)`

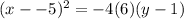
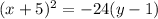
Or

`y=-(1)/(24)(x+5)^2+1`