Question

Arrange the cones in order from least volume to greatest volume.

a cone with a
diameter of 20
units and a
height of 12 units

a cone with a
diameter of 18
units and a height
of 10 units

a cone with a
radius of 10 units
and a height of
9 units

a cone with a
radius of 11 units
and a height of
9 units

Answer 1

847.8 cubic units , 942 cubic units , 1139.80 cubic units , 1256 cubic units

Step-by-step explanation:

The volume of cone is given as:
`\pi r^(2) (h)/(3)`

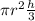
1. radius =
`20/2=10`

height = 12

So, volume =
`3.14*10*10* (12)/(3)`

= 1256 cubic units

2. radius =
`18/2=9`

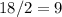
height = 10

So, volume =
`3.14*9*9* (10)/(3)`

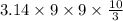
= 847.8 cubic units

3. radius = 10

height = 9

So, volume =
`3.14*10*10* (9)/(3)`

= 942 cubic units

4. radius = 11

height = 9

So, volume =
`3.14*11*11* (9)/(3)`

= 1139.80 cubic units

Now arranging these in least volume to greatest volume or ascending order.

847.8 cubic units , 942 cubic units , 1139.80 cubic units , 1256 cubic units

Answer 2

Answer: The required arrangement of volumes in increasing order will be

a) d) c) b)

Step-by-step explanation:

Since we have given that

cone with different diameters and heights all we need to do is to find the volume of cones :

As we know the formula for volume of cone which is given by

`Volume=(1)/(3)\pi r^2h`

a) Diameter = 20 units

Radius = 10 units

Height = 12 units

So, Volume is given by

`v=(1)/(3)* (22)/(7)* 10* 10* 12=1257.14\ cubic\ units`

b) Diameter = 18 units

Radius = 9 units

Height = 10 units

So, Volume is given by

`v=(1)/(3)* (22)/(7)* 9* 9* 10=848.57\ cubic\ units`

c) Radius = 10 units

Height = 9 units

So, Volume is given by

`v=(1)/(3)* (22)/(7)* 10* 10* 9=942.85\ cubic\ units`

d) Radius = 11 units

Height = 9 units

So, Volume is given by

`v=(1)/(3)* (22)/(7)* 11* 11* 9=1140.85\ cubic\ units`

So, the required arrangement of volumes in increasing order will be

a) d) c) b)