Question

Jacques needs to convert the function f(x) = x2 − 6x + 14 to vertex form, f(x) = (x − h)2 + k, in order to find the minimum.

When he does this, what is the value of k in the vertex form of function f?

A. 23
B. 9
C. 5
D. 14

Answer 1

C. 5

Explanation:

Given function is,

`f(x) = x^2 - 6x + 14`

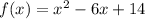
Here, the coefficient of x = 6,

Thus, We need to add and subtract the square of half of 6 in the given equation for getting the vertex form,

By adding and subtracting 9,

`f(x) = x^2 - 6x + 9 + 14 - 9`

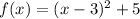`f(x) = (x-3)^2 + 5` ( Because, a² - 2ab + b² = (a-b)² )

Which is the required vertex form he will get,

By comparing it with
`f(x) = (x+h)^2+k`

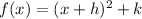
We get, k = 5,

⇒ Option C is correct.

Answer 2

k = 5

the equation of a parabola in vertex form is

y = a(x - h)² + k

where (h, k ) are the coordinates of the vertex and a is a multiplier

To obtain this form use the method of completing the square

Since the coefficient of the x² term is 1 then

add/ subtract (half the coefficient of the x-term )² to x² - 6x

f(x) = x² + 2(- 3)x + 9 - 9 + 14 = (x - 3)² + 5 → k = 5