Question

Find the equation of a line that goes through points (3,10) and (1,4)

Answer 1

To find the equation of the line, we have to find the slope of the line first. A slope of the line has two points of "x" as "x_1" and "x_2" and the second point of "y" as "y_1" and "y_2".

The two points in the graph are given as, (3, 10) and (1, 4).

The first line with the first points of variable "x_1" and "y_1" for the first line lying on those "x" and "y" planes is in this format; (x_1, y_1) = (3, 10). So, x_1 = 3 and y_1 = 2.

Similarly, for the second line with points of variable "x_2" and "y_2" for the second lying in those "x" and "y" planes in this format; (x_2, y_2) = (1, 4). So, x_2 = 1 and y_2 = 4.

Calculate the slope of the two given lines by the slope formula for slope between the two points in a graphical representation. That is:


`\boxed{\mathbf{Slope = (y_2 - y_1)/(x_2 - x_1)}}`


`\mathbf{Slope \: (m) = (4 - 10)/(1 - 3)}`


`\mathbf{m = (- 6)/(- 2)}`


`\boxed{\mathbf{Slope, \: m = 3}}`

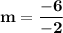
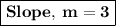
Find the equation of the two lines in a standard form of "y = mx + b". And put the value of slope, that is, "m" into the standard equation.


`\mathbf{y = 3 * x + b}`

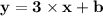
Put the value of points in the first or second line such as, "x_1, y_1" or "x_2, y_2". Both of the points of the given lines in a graph can provide the final values. Here, we are going to consider the first line of the following points as "x = 3" and "y = 10". Note that, you can even take the second line for a computation to find the value of "b" as well as complete the line equation. So:


`\mathbf{10 = 3 * 3 + b}`


`\mathbf{3 * 3 + b = 10}`


`\mathbf{9 + b = 10}`


`\mathbf{9 + b - 9 = 10 - 9}`


`\boxed{\mathbf{b = 1}}`

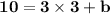
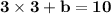
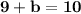
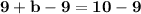
We have all the values for completing the line equation. By this, we can re-substitute the original values of "x" and "y" to confirm it is a correct line equation for two given lines.

Therefore, our line equation for a slope of "m = 3" and a variable point of "b = 1" is going to be:


`\boxed{\mathbf{\underline{y = 3x + 1}}}`

Hope it helps.