We are given parabola with vertex at origin (0,0) and given focus (0,-1).
We know vertex is given by (h,k).
Therefore, h=0 and k=0.
Formula for focus is (h, k + p).
On comapring with given focus
k+p = -1.
Plugging value of k=0 in above equation we get
0 +p =-1.
p = -1.
Parabola equation is 4p (y - k)=(x - h)^2
Plugging values of h, k and p in parabola equation, we get
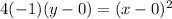
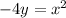
Dividing both sides by -4, we get
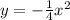 .
.
Therefore,
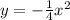 equation represents a parabola with a vertex at the origin and a focus at (0,-1).
equation represents a parabola with a vertex at the origin and a focus at (0,-1).