Answer:
28.1 m/s
Step-by-step explanation:
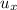 = Initial velocity of the fish = 1.52 m/s
= Initial velocity of the fish = 1.52 m/s
y = Height of the bird = 40 m
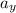 = Acceleration in y axis =
= Acceleration in y axis =
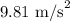
 = Initial velocity in y axis = 0
= Initial velocity in y axis = 0

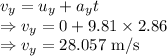
The final velocity in x direction will remain the same as the initial velocity as there is no acceleration in the x direction
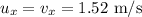
Resultant velocity is given by
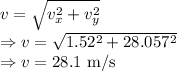
The fish is moving at a velocity of 28.1 m/s when it hits the water.