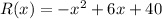Question

Please help, need answer fast!

The graph shows the daily revenue earned selling coupon cards in a fundraiser if the price is decreased by x dollars.


Which function can be used to determine the daily revenue if the price of a coupon card is decreased by x dollars?

Answer 1

Answer:A on edge:)

Explanation:

Answer 2

From given graph we see that points forms a parabolic shape that means we can use quadratic model to find the equation whose formula is given by:

`y=a(x-h)^2+k`

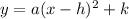
where (h,k) represents vertex.

From graph we see that vertex is (3,49).

Hence h=3 and k=49

Plug these values into above formula

we get:

`y=a(x-3)^2+49`

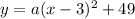
Now we need to find the value of a, so we can plug any point say (5,45) then we get:

`45=a(5-3)^2+49`

`45=a(2)^2+49`

`45=4a+49`

`45-49=4a`

`-4=4a`

`-1=a`

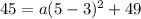
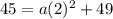
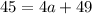
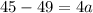
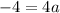
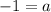
Plug value of a, h and k into above formula, we get:

`y=-1(x-3)^2+49`

`y=-1(x^2-6x+9)+49`

`y=-x^2+6x-9+49`

`y=-x^2+6x+40`

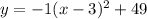
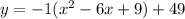
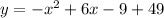
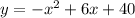
which best matches with first choice

Hence final answer is
`R(x)=-x^2+6x+40`